POTENCIACION
Por: JENNY NAULA SUMBA
La potenciación es una operación
matemática entre dos términos denominados: base a y
exponente n. Se escribe an y se lee
usualmente como «a elevado a n» o «a elevado
a la n» y el sufijo en femenino correspondiente al exponente n.
Hay algunos números especiales, como el 2, al cuadrado o el 3,
que le corresponde al cubo. Nótese que en el caso de la
potenciación la base y el exponente pueden pertenecer a conjuntos diferentes,
en un anillo totalmente general la base será un elemento del anillo
pero el exponente será un número natural que no tiene porqué
pertenecer al anillo. En un cuerpo el exponente puede ser un número
entero o cero.
Definición
Se llama potencia a una expresión de la forma , donde a es
la base y n es el exponente. Su
definición varía según el conjunto numérico al que pertenezca el
exponente.
, donde a es
la base y n es el exponente. Su
definición varía según el conjunto numérico al que pertenezca el
exponente.
Exponente entero
Cuando el exponente es un número natural n,
este indica las veces que aparece a multiplicando por sí
mismo, siendo a un número cualquiera:
(1)
Multiplicación de potencias de igual base
El producto de dos potencias que tienen la misma base es igual a una potencia de dicha base que tiene como exponente la suma de los exponentes, es decir

Potencia de una potencia
La potencia de una potencia de base a es igual a la potencia de base a y cuyo exponente es el producto de ambos exponentes (la misma base y se multiplican los exponentes)
Debido a esto, la notación  se reserva para significar
se reserva para significar 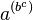 ya que
ya que  se puede escribir sencillamente como
se puede escribir sencillamente como 
 se reserva para significar
se reserva para significar 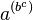 ya que
ya que  se puede escribir sencillamente como
se puede escribir sencillamente como 
Potencia de un producto
La potencia de un producto es igual al producto de cada uno de los factores elevado al mismo exponente, es decir
Se suman los exponentes
División de potencias de igual base
El cociente de dos potencias con la misma base es igual a una potencia de dicha base con un exponente igual a la diferencia del exponente del dividendo menos el del divisor ,esto es:
 |
Ejemplo:
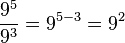
- Se restan los exponentes
Potencia de exponente 0
Un número distinto de 0 elevado al exponente 0 da como
resultado la unidad (1), puesto que:
El caso particular de 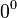 , en principio, no está definido.
, en principio, no está definido.
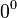 , en principio, no está definido.
, en principio, no está definido.Potencia de un cociente
La potencia de un cociente es igual al cociente de cada uno de los números elevado al mismo exponente.
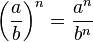 |
Exponente racional
La potenciación con exponente racional viene de la necesidad de resolver una ecuación del tipo  , de manera que
, de manera que ![x = \sqrt[n]{a}](https://upload.wikimedia.org/math/4/6/9/469c5e753bca6920bc3a41f0f2cbf136.png) , pero se ha de garantizar que dicha x sea un numero real y esto sólo se puede garantizar para toda n si la base a es un número real positivo, por lo que existe un teorema que dice:
, pero se ha de garantizar que dicha x sea un numero real y esto sólo se puede garantizar para toda n si la base a es un número real positivo, por lo que existe un teorema que dice:
 , de manera que
, de manera que ![x = \sqrt[n]{a}](https://upload.wikimedia.org/math/4/6/9/469c5e753bca6920bc3a41f0f2cbf136.png) , pero se ha de garantizar que dicha x sea un numero real y esto sólo se puede garantizar para toda n si la base a es un número real positivo, por lo que existe un teorema que dice:
, pero se ha de garantizar que dicha x sea un numero real y esto sólo se puede garantizar para toda n si la base a es un número real positivo, por lo que existe un teorema que dice:Dado un número real positivo a, este tiene una única raíz n-ésima positiva. |
Para notar la raizse define el uso de fracciones en el exponente:
(3)
- Observación
En general para las fracciones se define que:
(4)
- Relación
  |
Propiedades
Exponente real
La potenciación puede extenderse a exponentes reales usando sucesiones racionales; esto se recoge en el siguiente teorema:
Dado un número real positivo a y una sucesión de números racionales |
Nótese que las sucesivas aproximaciones de ab tienen como exponente números racionales, con lo que para que la definición sea consistente, se exige que a sea un número real positivo.
Análogamente, se puede extender la potenciación a funciones, usando la funcion exponencial, y su inversa, la función logaritmo natural, en un proceso que se denomina exponenciacion. Así, se define
 .
.
De igual manera, esta es totalmente consistente si el conjunto imagen de f(x) es el conjunto de los números reales positivos R+, o algún subconjunto de este, siendo los valores de la función exponente g(x) números reales cualesquiera, debido a que el logaritmo natural no está definido para números negativos.
Propiedades
Exponente complejo
Puede extenderse a exponentes complejos usando funciones analíticas o holomorfas, así  donde det-exp es la determinación de la exponencial y det-log la determinación del logaritmo.
donde det-exp es la determinación de la exponencial y det-log la determinación del logaritmo.
 donde det-exp es la determinación de la exponencial y det-log la determinación del logaritmo.
donde det-exp es la determinación de la exponencial y det-log la determinación del logaritmo.Resultados de potenciación
Propiedades que no cumple la potenciación
No es distributiva con respecto a la adición y sustracción (véase productos notables), es decir, no se puede distribuir cuando dentro del paréntesis es suma o resta:
No cumple la propiedad conmutativa,exceptuando aquellos casos en que base y exponente tienen el mismo valor o son equivalentes. En general:
Tampoco cumple la propiedad asociativa:
Potencia de base 10
Para las potencias con base 10 y exponente entero,el efecto será desplazar la como decimal tantas posiciones como indique el exponente, hacia la izquierda si el exponente es negativo, o hacia la derecha si el exponente es positivo.
Ejemplos:
En la siguiente pagina web puedes revisar lo explicado.
Puedes encontrar mas información de las propiedades de la potenciacion accediendo a los siguientes videos.
En el siguiente video podrás encontrar ejemplos de potencias de base 10.





![a^{\frac{1}{n}} = \sqrt[n]{a}](https://upload.wikimedia.org/math/c/d/e/cde604330dc8b9bb773376cb1fbf2098.png)

![\begin{array}{ll}
a^{\frac{n}{m}} & = \sqrt[m]{a^n} \\
a^{-\frac{n}{m}} & = \frac{1}{ a^{\frac{n}{m}} }
\end{array}](https://upload.wikimedia.org/math/2/6/0/26012d17329f505126092fc86d5f7553.png)


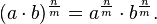
 que tiene límite
que tiene límite  que se escribe como:
que se escribe como:


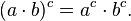
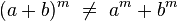
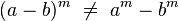


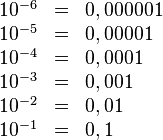
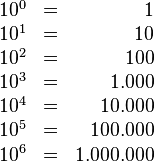
No hay comentarios:
Publicar un comentario